unidad 5
Interpolacion de Newton
Se basa en la obtención de un polinomio a partir de un conjunto de puntos dado, aproximándose lo mas posible a la curva buscada.
Donde las “bi” se obtienen mediante la aplicación de una serie de funciones incluidas en una tabla de diferencias.
Interpolación segmentada
Esta interpolación se llama interpolación segmentaria o interpolación por splines. La idea central es que en vez de usar un solo polinomio para interpolar los datos, podemos usar segmentos de polinomios y unirlos adecuadamente para formar nuestra interpolación.
Cabe mencionar que entre todas, las splines cúbicas han resultado ser las más adecuadas para aplicaciones como la mencionada anteriormente.
Así pues, podemos decir de manera informal, que una funcion spline está formada por varios polinomios, cada uno definido en un intervalo y que se unen entre si bajo ciertas condiciones de continuidad.
POLINOMIOS DE INTERPOLACIÓN DE LAGRANGE
El polinomio de interpolación de Lagrange, simplemente es una reformulación del polinomio de Newton que evita los cálculos de las diferencias divididas. Este se puede representar concretamente como:
| (21) |
en donde:
| (22) |
En donde denota el "producto de".
denota el "producto de".
Por ejemplo, la versión lineal (n = 1) es:
| (23) |
y la versión de segundo orden es:
| (24) |
al igual que en el método de Newton, la versión de Lagrange tiene un error aproximado dado por:
| (25) |
La ecuación (21) se deriva directamente del polinomio de Newton. Sin embargo, la razon fundamental de la formulación de Lagrange se puede comprender directamente notando que cada término Li(X) será 1 en X=Xi y 0 en todos los demas puntos.
Por lo tanto, cada producto Li(X) f(Xi) toma un valor de f(Xi) en el punto Xi. Por consiguiente la sumatoria de todos los productos, dada por la ecuación (21) es el único polinomio de n-ésimo orden que pasa exactamente por los n+1 puntos.
CORRELACIÓN
La finalidad de la correlación es examinar la dirección y la fuerza de la asociación
entre dos variables cuantitativas. Así conoceremos la intensidad de la relación entre
ellas y si, al aumentar el valor de una variable, aumenta o disminuye el valor de la otra
variable.
Para valorar la asociación entre dos variables, la primera aproximación suele hacerse
mediante un diagrama de dispersión.
El análisis de regresión es una técnica
estadística para investigar la relación
funcional entre dos o más variables,
ajustando algún modelo matemático.
El método de mínimos cuadrados
permite ajustar los datos observados
a la línea recta este ajuste se
obtendrá minimizando el erro entre los
puntos estimados y los puntos
observados.
Aplicaciones
Ingeniería y Diseño (CAD/CAM, CNC’s)frecuencia Geología Aeronáutica y automoción Economía Procesamiento de señales e imágenes (Reconocimiento de patrones, recuperación de imágenes) Robótica Medicina (Aparatos auditivos, mapas cerebrales) Meteorología (Mapas climáticos, detección de inundaciones,...)
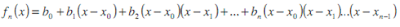

Comentarios
Publicar un comentario